Atmospheric component

The atmospheric component is a two-layer quasi-geostrophic (QG) atmosphere in the beta-plane approximation. The atmospheric component is an extension of the QG model, first developed by [AC-CS80] and further refined by [AC-RP82] and [AC-CT87].

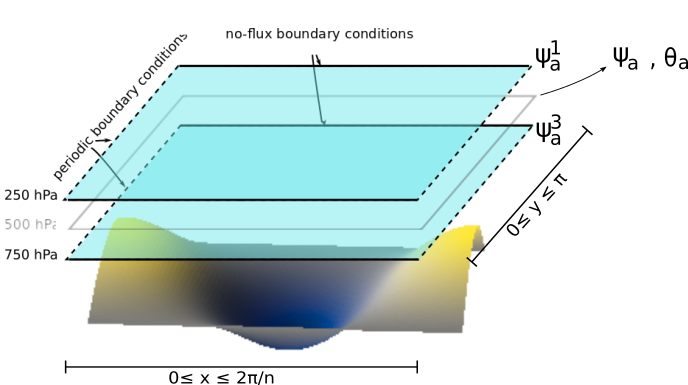
Sketch of the atmospheric model layers with a simple orography. The domain (\(\beta\)-plane) zonal and meridional coordinates are labeled as the \(x\) and \(y\) variables.

The equations of motion for the atmospheric streamfunction fields \(\psi^1_\text{a}\) at 250 hPa and \(\psi^3_\text{a}\) at 750 hPa, and the vertical velocity \(\omega = \text{d}p/\text{d}t\), read

\[\begin{split}\frac{\partial}{\partial t} \overbrace{\left(\nabla^2 \psi^1_{\rm a}\right) }^{\text{vorticity}}+ \overbrace{J(\psi^1_{\rm a}, \nabla^2 \psi^1_{\rm a})}^{\text{horizontal advection}} + \overbrace{\beta \frac{\partial \psi^1_{\rm a}}{\partial x}}^{\beta\text{-plane approximation} \\ \text{of the Coriolis force}} & = \overbrace{-k'_d \nabla^2 (\psi^1_{\rm a}-\psi^3_{\rm a})}^{\text{friction}} + \overbrace{\frac{f_0}{\Delta p} \omega}^{\text{vertical stretching}} \nonumber \\ \frac{\partial}{\partial t} \left( \nabla^2 \psi^3_{\rm a} \right) + \, \ J(\psi^3_{\rm a}, \nabla^2 \psi^3_{\rm a}) \, \ + \qquad \beta \frac{\partial \psi^3_{\rm a}}{\partial x} \qquad & = +k'_d \nabla^2 (\psi^1_{\rm a}-\psi^3_{\rm a}) - \quad \ \frac{f_0}{\Delta p} \omega \nonumber \\\end{split}\]

where \(\nabla^2\) is the horizontal Laplacian. The Coriolis parameter \(f\) is linearized around a value \(f_0\) (f0) evaluated at latitude \(\phi_0\) (phi0_npi), \(f = f_0 + \beta y\), with \(\beta=\text{d}f/\text{d}y\) (beta). The parameter \(k'_d\) (kdp) quantify the friction between the two atmospheric layers, and \(\Delta p = 500\) hPa (deltap) is the pressure difference between the atmospheric layers. Finally, \(J\) is the Jacobian \(J(S, G) = \partial_x S\, \partial_y G - \partial_y S\, \partial_x G\).

References

AC-CT87

P. Cehelsky and K. K. Tung. Theories of multiple equilibria and weather regimes - A critical reexamination. Part II: Baroclinic two-layer models. Journal of the Atmospheric Sciences, 44(21):3282–3303, 1987. URL: https://doi.org/10.1175/1520-0469(1987)044%3C3282:TOMEAW%3E2.0.CO;2.

AC-CS80

J. Charney and D. Straus. Form-drag instability, multiple equilibria and propagating planetary waves in baroclinic, orographically forced, planetary wave systems. Journal of the Atmospheric Sciences, 37(6):1157–1176, 1980. URL: https://doi.org/10.1175/1520-0469(1980)037%3C1157:FDIMEA%3E2.0.CO;2.

AC-RP82

B. Reinhold and R. Pierrehumbert. Dynamics of weather regimes: quasi-stationary waves and blocking. Monthly Weather Review, 110:1105–1145, 1982. URL: https://doi.org/10.1175/1520-0493(1982)110%3C1105:DOWRQS%3E2.0.CO;2.